高中数学课堂中问题导向教学法的应用探索

福建省漳平第一中学 364400

摘要：摘要：高中数学课堂中，问题导向教学法应用需遵循问题导向、学生参与、发现性学习及最近发展区原则。教师应设计代表性问题，激发学生求知欲，引导学生积极参与问题解决。策略上，可运用留白艺术抛出问题，设计问题链引导持续探索，并进行问题反思与回顾，以深化理解、巩

关键词：

高中数学；问题导向；应用

出处：

《教育研究》2024年13期

DOI：
10.13738/j.cnki.acc.qklw60536
专辑：
科学Ⅰ辑;信息科技
专题：
信息、科学;综合科技
分类号：
G90;N92

摘要：高中数学课堂中，问题导向教学法应用需遵循问题导向、学生参与、发现性学习及最近发展区原则。教师应设计代表性问题，激发学生求知欲，引导学生积极参与问题解决。策略上，可运用留白艺术抛出问题，设计问题链引导持续探索，并进行问题反思与回顾，以深化理解、巩固知识。

关键词：高中数学；问题导向；应用

引言：在高中数学教学中，引入问题导向教学法具有重要意义。通过遵循特定原则，教师能有效引导学生探索数学知识，培养数学思维与问题解决能力。本文旨在探讨问题导向教学法在高中数学课堂中的应用原则与策略，以期为提高数学教学质量提供参考。

一、高中数学课堂中问题导向教学法的应用原则

在高中数学课堂里，教师若要引入问题导向教学法，理应遵循如下原则。首先，教师应以问题作为起始点，着重强调问题乃是教学的出发点与核心所在，严格秉持问题导向原则，引领学生去攻克实际问题。在这一进程中，致力于培育学生的数学思维以及解决问题的能力。课堂之上，教师主要任务是精心设计具备代表性与针对性的数学问题，此类问题要能够充分激发学生的学习兴趣与求知欲。学生作为学习的主体，教师应积极引导他们踊跃参与到问题的解决过程之中，切实奉行学生参与性原则，促使学生去深入分析问题、大胆提出假设并巧妙设计解决方案。这一过程能够极大地激发学生的思考与探索精神。此外，教师还应始终坚守发现性学习原则，也就是引导学生在解决问题的过程中自主探寻知识、掌握技能。为此，教师可通过巧妙设置悬念、抛出具有挑战性的问题，以此来点燃学生的好奇心与求知欲。最后，教师必须尊重学生的发展规律，依据最近发展区原则，结合建构主义理论，参照学生的知识水平来精心构建问题。务必确保问题设计具备层次性与梯度性，从而保障学生能够持续深入地学习。

二、高中数学课堂中问题导向教学法的应用策略

（一）基于留白艺术抛出问题

问题的引入，务必充分调动学生的兴趣与探索欲望，如此方能收获更为理想的教学成效。故而，教师可借助留白艺术来抛出问题，有效激发学生的好奇心。所谓留白艺术，主要是指教师在教学过程中，如同艺术创作一般，有意留下空白或未完成的部分，以此激发学生的探究热情与参与度。在教学时，教师并非直接给出答案或完整的解决思路，而是通过巧妙提出问题或设置悬念，引导学生自主思考与探索。这种教学方法以问题为核心驱动力，助力学生提升分析问题、提出解决方案并最终解决问题的能力。教师将留白艺术与问题导向教学法有机融合，能够切实减轻学生的学习负担，同时极大地激发他们的学习兴趣。在实践过程中，教师需精心创设一个与数学知识紧密相关的问题情境，该情境应蕴含实际性与趣味性元素，以此吸引学生的注意力。随后在情境描述中，特意预留一些思考空间与悬念，让学生感觉到问题并非轻而易举就能解决，而是需要经过一番深入思考才行。这样的问题能够充分激发学生的求知欲。同时，教师还可抛出不完整的问题，有意使问题残缺或模糊，让学生心生困惑与好奇。之后促使学生通过合作探讨或独立思考，对问题进行补充与完善。不过，教师所设定的留白空间务必适度适量。倘若留白设计过多，会致使学生在探索问题时偏离主线方向；若留白设计过少，则难以达到良好的启发效果。

例如，数列知识在生活中有着广泛应用，教师便以此为切入点，精心创设了一个与生活紧密相关的问题情境。比如，在讲解等比数列时，教师描述道：“同学们，想象一下，我们现在有一个神奇的折纸过程。假设一张纸的厚度为0.1毫米，每次对折后，纸张的厚度都会翻倍。”这里，教师通过生动的描述，将学生带入一个充满趣味的情境中，吸引了他们的注意力。接着，教师并没有直接给出后续的问题，而是留下了悬念：“那么随着对折次数的不断增加，你们猜猜纸张厚度会发生怎样令人惊讶的变化呢？”这个悬念就如同留白，让学生们开始在脑海中积极思考，激发了他们的好奇心和求知欲。随后，教师进一步抛出不完整的问题：“当对折了若干次后，纸张的厚度达到了一个数值，但是我现在不告诉你们对折了几次，只知道这个厚度已经超过了珠穆朗玛峰的高度，大家想想，我们该怎么去计算这个对折次数呢？”这个问题残缺不全，学生们一下子陷入了困惑与好奇之中，急切地想要通过自己的思考去补充完整并解决问题。

（二）设计问题链引导持续性探索

高中数学教师在引入问题导向法时，不妨尝试设计问题链，以支持学生展开持续性探究。问题链主要是指设计一系列相互关联且层次递进的问题，它们共同构建起一个完整的问题体系，用以引导学生逐步完成学习探究。在问题的引导下，学生不断发现问题、分析问题并解决问题。在实践环节，教师首先需明确教学目标与核心内容，进而确定问题的起点与终点，以及中间各个环节的关联性与递进性。随后，教师要构建问题链的框架，这包括确定问题链的层次结构、问题之间的逻辑关系以及每个问题的具体表述。整个问题链的层次结构应清晰明了，从简单到复杂、从具体到抽象逐步递进。问题之间的逻辑关系也应紧密相连，形成一个有机整体。每个问题都要有确切的表述。然而，问题链的设计并非一成不变，教师需依据学生回答上一个问题时的实际表现，灵活设计下一个问题，以更好地贴合学生的实际学习需求，灵活把控问题，确保学生朝着正确的目标与方向前行。

例如，在高中数学函数单调性的教学中，教师巧妙运用问题导向法，精心设计问题链，引领学生开启一段深入的持续性探索之旅。

首先，教师明确教学目标是让学生透彻理解函数单调性的概念，并能熟练运用其判断函数的单调性。基于此，教师确定问题的起点为学生已熟悉的简单函数图像，终点则是学生能够自主准确判断复杂函数的单调性。

教师开启问题链的第一环：“同学们，我们先来看一次函数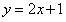高中数学课堂中问题导向教学法的应用探索(图1) 的图像，仔细观察，从左往右看，函数图像呈现出怎样的变化趋势呢？”这个简单直观的问题，引导学生将目光聚焦在熟悉的函数图像上，轻松迈出探索的第一步。学生们迅速观察并纷纷回答图像是上升的。

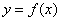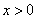紧接着，教师抛出第二个问题：“那对于反比例函数高中数学课堂中问题导向教学法的应用探索(图2) ，在高中数学课堂中问题导向教学法的应用探索(图3) 的区间内，图像又有着怎样不同的变化呢？”这一问题在第一个问题的基础上，巧妙转换到另一类函数，且限定了区间，增加了些许难度，促使学生进一步思考函数在不同区间的变化情况。学生们认真观察后，发现图像是下降的。

随后，教师提出更具深度的问题：“我们把刚才观察到的函数图像上升或下降的这种特性，用数学语言该如何准确描述呢？”此问题从具体的函数图像观察，过渡到抽象的数学语言表达，让学生从直观感知迈向理性认知，将探索引向深入。学生们开始热烈讨论，尝试用自己的语言去概括。

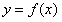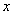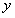当学生们初步给出描述后，教师继续追问：“那对于一般的函数高中数学课堂中问题导向教学法的应用探索(图4) ，如果在某个区间I上，随着高中数学课堂中问题导向教学法的应用探索(图5) 值的增大，高中数学课堂中问题导向教学法的应用探索(图6) 值也始终增大，我们可以说函数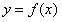高中数学课堂中问题导向教学法的应用探索(图7) 在区间I上具有什么性质呢？”这个问题进一步抽象和升华，引导学生从特殊函数的特性归纳出一般函数单调性的概念。

在学生对函数单调性概念有了初步理解后，教师又灵活根据学生的掌握情况，提出新问题：“现在已知函数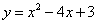高中数学课堂中问题导向教学法的应用探索(图8) ，你们能试着找出它的单调区间，并说明理由吗？”这一问题将理论知识应用到具体函数的分析上，检验学生对概念的理解与运用能力。

（三）问题反思与回顾

问题导向教学法应当具备一个完整的闭环结构。倘若仅仅进行过程性指引，却不进行总结反思，就难以取得良好的教学效果。因此，教师在引导学生完成问题探索之后，应当引导他们对问题进行深入思考与总结，以此深化理解、巩固知识、提升能力。其中，教师可引领学生在解决问题之后进行自我提问，例如：为何会采用这种解决方法？这种方法的适用范围是什么？借此促使学生思考问题的本质，夯实对知识的理解记忆。并且，学生在解决问题的过程中难免会出错，针对这些错误，学生应在后续认真分析出错原因，究竟是概念理解不清晰、公式记忆错误，还是计算出现失误等，从而发现自己的薄弱环节。学生在解决问题之后，还应当总结问题的规律与解决方法。比如，对于某一类数学问题，学生可总结其解题步骤与技巧，这样在遇到类似问题时，便能迅速找到解决方案。为了简化学生回顾总结问题的分析过程，教师可以运用时间轴线或思维导图，帮助学生梳理反思记录，整理解决问题的整个过程，并将相关信息罗列整合在一起，利用连线串接，构建起一个完整的问题框架。从这个问题框架中剖析出一般性的知识规律与概念，进而提高学习效率。

比如，在学生成功运用定义法判断出函数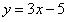高中数学课堂中问题导向教学法的应用探索(图9) 的单调性后，教师启发学生思考：“为啥咱们要用定义法来判断这个函数的单调性呢？”学生们经过思考，意识到定义法是判断函数单调性的基础且通用的方法，适用于各种函数类型的单调性判断。接着，教师又引导：“那这种定义法在什么情况下运用起来最为顺手呢？”学生们进一步总结出，当函数形式较为简单，能够直接通过比较自变量与函数值的变化关系时，定义法就很适用。通过这样的自我提问，学生们深入思考了问题解决方法的本质，让函数单调性的知识在脑海中扎根更深。