数形结合——学透近似数的理与法——求小数近似数的教学设计反思

【摘 要】 小数近似数的常规教学理念中，只需要引导学生将求整数近似数的知识经验迁移到求小数近似数的新情境中，就可以顺利解决求小数近似数的问题。但此教学操作重技法的指导轻算理的理解，学生学习中会存在3个普遍性的疑问。为什么要与“5”作比较？为什么只需要省略部分的最高位与5进行比较？求得的近似数是小数且末尾有“0”，“0”为何不能去掉？

【关键词】小数的近似数；数轴；数形结合；

小数的近似数这一知识点是人教版数学四年级下册第四单元的学习内容。小学阶段关于近似数知识的安排有的是以例题形式显性安排，有的是以习题形式隐性出现。学生学习近似数经历了4个阶段。阶段1：低段初步感知近似数，例如，58更接近50还是更接近60；阶段2：四年级上册学习除数是两位数的除法时，采用“四舍五入”法将除数看成与之接近的整十数，是近似数的实操学习；除段3：四年级上册学习将一个整数和改写成用“万”或“亿”作单位并按要求求出近似数，此时的学习已经是关于近似数知识的显性安排；除段4：小数的近似数的学习，同样是关于近似数知识的显性安排。

由此看来，在学习本节课的新知识之前，学生已经积办了非常丰富的有关近似数的实操经验，同时也在上学期学习了求整数近似数的知识，知道了求近似数的“理”是四舍五入。所以，在常规教学理念中，只需要引导学生将求整数近似数的知识经验迁移到求小数近似数的新情境中，就可以顺利解决求小数近似数的问题。但这种教学操作重技法的指导轻算理的理解，实际教学中，学生学习中会存在3个普遍性的疑问。问题1：为什么要与“5”作比较？问题2：为什么只需要省略部分的最高位与5进行比较？问题3：求得的近似数是小数且末尾有“0”，“0”为何不能去掉？

一、基于上述疑问，如何才能让学生更好的理解近似数，并能够清楚明晰的解决近似数的问题呢？针对这一教学难点，实际教学实践中，将数轴引入课堂，数形结合，化抽象为形象，引导学生通过对数轴上数与数之间关系的观察，将求整数近似数的方法迁移至小数中。同时，借助数轴，数形结合，解决学生的3个疑问，突破认识困难，真正掌握求小数近似数的算理与算法。

二、借助数轴，理解要与中间数“5”进行比较

教学情境：

选用人教版四上第1单元例7的内容进行导入，实际教学中，为了突出对比，将李阿姨的总步数改为188309，近似数改为19万步。

张阿姨与李阿姨在交流4月份的总步数，张阿姨的总步数是182068，李阿姨的总步数是188309。在交流中，张阿姨说自己走了大约18万步，李阿姨说自己走了大约19万步。

知识背景分析：

在此之前，学生已学过整万数的改写，但此题呈现的不是整万数，自然而然想到要分析这两个数字分别更接近哪个整万数。由此联想到求近似数的知识点。182068与188309这两个数在180000与190000之间，改写成以万为单位的数后是18万或19万，结果是什么？

依据是什么？此时，呈现数轴，标出180000与190000这两个整万数，并将它们之间的线段平均分成10份。提出如下问题，形象解决问题。

问题1：观察数轴，哪些数字更接近180000，哪些数字更接近190000？

教学实录反思：

大部分同学会看到181000、182000......，因为数轴的呈现方式就是把这两个整万数之间的线段平均分成的十份；少数同学会意识要这两数之间数的无限性，会有类似181999、182032......的数出现，甚至还会出现小数，小数的出现是非常值得肯定的生成。同学们在此环节互相碰撞，说出越来越来符合要求的数。

问题2：判断依据是什么？

教学实录反思：

大部分同学都提到要与185000进行比较，大于等于185000的数就会靠近190000，小于185000的数就会靠近180000。这个回答并未触及问题的本质。直到有同学说出因为185000与180000和190000的差一样，才开始触及问题的本质。靠近谁的提法，实际上就是看差值，用减法来进行验证。用数轴对算理进行简化，185000是中间数，到180000与190000的距离是一样的，由运算到数轴，由数到形，最终于实现用形解释数，帮助学生形成数学直观能力——数形结合。

三、通过对比，理解为什么只需将省略部分最高位与“5”作比较

问题1：创设认知冲突，激发思考。同样是18万多，为什么一个约等于18万，一个约等于19万？谁起了关键作用？

呈现数轴，将180000与190000之间的线段平均分成10份。标记182068与188309。

教学实录反思：

此时，学生知道要用两个数与185000进行比较，因为188309大于185000，所以约等于190000，而182068小于185000，所以约等于180000。这样的理由实际还是模糊的，所以将问题再次细化，与185000比较的依据是什么？此时，学生会去想，进行比较的逻辑，因为十万位与万位都是相同的，比较的是千位，而千位正是要省略部分的最高位。千位后面的数对于近似数的结果没有影响。同时要求学生再分别列举出近似数是190000的数，验证刚刚得出的结论。

教学创新点：划线点点法求近似数。

当学生们知道求近似数的理时，要适当的总结技法。在实际的教学中，总结出划线点点求近似数法。

划线：区分保留部分与省略部分。

点点：点点在省略部分的最高位。

经过两个操作，让求近似的理以可视化的操作外显出来，更能让学生理解求近似数的理。

四、经验迁移：求小数的近似数

人教版的教材是以生活中常见的身高记录值为情境引入这一学习内容的。小欣的身高是0，984m，表述1：小欣的身高约是0.98m。表述2：小欣的身高约是1m。

在接下来的探究环节里，出示的是保留两位小数与保留一位小数的探讨过程，与学生原有知识有割裂，实际教学中，先探究更接近哪个整数的问题。

问题1：0.98更接近哪个整数？

教学实录反思：

学生很容易想出0.98在0与1两个整数间，同时定位到中间数0.5。呈现数轴，标记0与1，并将0与1之间的线段平均分成10，呈现中间数0.5。

学生容易得出结论，0.98≈1。在实际教学中要追问，得出结果1的依据。必须要有9大于5，所以要先向前一位进“1”再省略的表述。

要求学生分别举出近似数是1的一位小数，三位小数，四位小数......，深化省略部分最高位对近似数的结果起决定作用的道理。

操作方法展示：

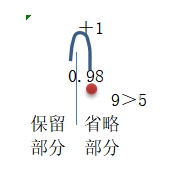
问题是0.98接近哪个整数，所以保留的是整数部分，

省略的是小数部分，小数部分的最高位是9，9大于5，

先向个位进“1”后再省略。

问题2：将0.984保留两位小数。

教学实录反思：

问题2变换了提问题方式，需要学生理解“保留”是什么意思。由原来的三位小数，最终变成二位小数，从要求上，学生要理解本题是要求近似数，进而理解是找到最接近0.984的两位小数。由此，学生知道，0.984在0.98与0.99这两个两位小数之间，最终结果是0.98还是0.99，起决定作用的是千分位上的4。此时，他们完全可以在头脑中构建数轴，标记数值，得出结果0.98。

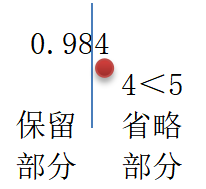
操作方法展示：

0.984，保留二位小数，

那么保留部分是0.98，省略部分是千分位上的

4，并且4要与5进行比较，小于5，直接将省略部分舍去。

四、借助数轴，理解小数的近似数末尾的“0”不可以去掉，进而理解精确度。

问题3：将0.984保留一位小数。

教学实录反思：

学生自主完成，要求讲明道理与操作方法。答案有1与1.0。学生在解释为什么是1时，用到了小数的性质；在解释为什么不能是“1”时，提到题目的要求是保留一位小数。接下来的问题就是深入研究为什么必须是1.0的道理。研究此问题，借助两个小问题来进行深入研究。

问题4：哪些数的近似数是1？

问题5：哪些数的近似数是1.0？

教学实录反思：

两个问题的教学目的是让学生确定近似数是1及1.0的原始数据分布范围，通过对比发现这两个近似数的原始数据的分布范围是不一样的，进而明白近似数是“1.0”和“0”是不可以去掉的。

当学生说出一位小数时继续问有没有可能是两位小数，再追问，最后得出论，原始数据有无数个。近似数是1的原始数在0.9-1.4（1.0除外，包含0.9及1.4）之间，近似数是1.0的原始数在0.95-1.04（1.00除外，包含0.95及1.04）之间，同时标记出这个范围。

通过对比，学生发现，两个近似数的原始数据分布范围不同。近似数是1.0的原始数据范围要比近似数是1的原始数据的范围要小。通过数轴上数据的分布，学生理解，如果去掉了近似数是小数的末尾的“0”，会直接影响到原始数据分布范围，所以近似数是小数的末尾的“0”不可以去掉。

同时，以班级平均分举例，保留整数时是90分，保留一位小数是是90.4分，保留两位小数时是90.44分。我们更愿意以哪个作为自己班的平均分。愿意以90.44分作为自己班的平均分，一个角度就是比较大小，90.44更大一些。一个是90.44更接近班级的真实水平，从数学专业术语角度上来说，就是精确度高，适时引入，当计数单位越小时，数字的精确度越高，越接近所要描述的实际情况。所以近似数1.0的“0”代表的是它的精确度，不可去掉。

本次教学设计，借助数轴，解决学生学习求近似数的3个认知困难，学生更加理解求近似数的算理。数量关系获得几何解释，可以使问题变得直观易懂，使学生易于洞察问题的本质。

参考文献

[1]徐文彬.数形结合思想的历史发展、思维意蕴与教学价值[J].小学数学教育，2015（5）：3-5.

[2]章勤琼. 3.8是3.80的近似数吗：近似和估算教学的关键是什么［J］. 教学月刊·小学版（数学），2019（4）：60-63.

[3]张雅芬.巧借数轴 探其本质：“求小数的近似数”片段赏析［J］.数学学习与研究，2015（19）：87，89.